椭圆习题
前言
技巧:为了避免焦点在哪个坐标轴的分类讨论,我们可以统一设椭圆的标准形式为 \(mx^2+ny^2=1\),\((m>0,n>0)\);
典例剖析
法1:若不知道焦点所在的位置,我们一般是分类讨论精确设标准形式,如设焦点在 \(x\) 上的标准形式:\(\cfrac{x^2}{a^2}\)\(+\)\(\cfrac{y^2}{b^2}\)\(=\)\(1\),\((a>b>0)\) 和焦点在 \(y\) 轴上的标准形式:\(\cfrac{x^2}{b^2}\)\(+\)\(\cfrac{y^2}{a^2}\)\(=\)\(1\),\((a>b>0)\) 两种分别求解;求解略;
法2:不知道焦点所在的位置,也可以笼统设椭圆的标准形式为 \(mx^2+ny^2=1\),\((m>0,n>0)\)焦点在 \(x\) 上的标准形式:\(\cfrac{x^2}{a^2}\)\(+\)\(\cfrac{y^2}{b^2}\)\(=\)\(1\),\((a>b>0)\) ,若设 \(m\)\(=\)\(\cfrac{1}{a^2}\) , \(n\)\(=\)\(\cfrac{1}{b^2}\) ,则其标准形式变化为\(mx^2\)\(+\)\(ny^2\)\(=\)\(1\),\((m>0\)\(,\)\(n>0\)\(,\)\(n>m)\),焦点在 \(y\) 轴上的标准形式:\(\cfrac{x^2}{b^2}\)\(+\)\(\cfrac{y^2}{a^2}\)\(=\)\(1\),若设 \(m\)\(=\)\(\cfrac{1}{b^2}\) , \(n\)\(=\)\(\cfrac{1}{a^2}\) ,则其标准形式变化为\(mx^2\)\(+\)\(ny^2\)\(=\)\(1\),\((m>0\)\(,\)\(n>0\)\(,\)\(m>n)\),故将两种形式可以统一抽象为 \(mx^2\)\(+\)\(ny^2\)\(=\)\(1\),\((m>0\)\(,\)\(n>0)\),不再限制\(m\) 与\(n\) 的大小关系,此时就能包含两种形式;
法2:为了避免分类讨论,设椭圆的标准形式为 \(mx^2+ny^2=1\),\((m>0,n>0)\),则由椭圆上的两点 \((2,-\sqrt{2})\) 和 \((-1,\cfrac{\sqrt{14}}{2})\),可知
\(\left\{\begin{array}{l}{4m+2n=1}\\{m+\cfrac{14n}{4}=1}\end{array}\right.\quad\),解得 \(\left\{\begin{array}{l}m=\cfrac{1}{8}\\n=\cfrac{1}{4}\end{array}\right.\),
故椭圆的标准方程为 \(\cfrac{x^2}{8}+\cfrac{y^2}{4}=1\), 此时由计算得到的 \(m\) 和 \(n\) 的大小来决定焦点所在的位置。

分析:由题可知,\(a=3\),如图所示,由椭圆的定义可知\(|AF_1|+|AF_2|=2a\),\(|BF_1|+|BF_2|=2a\),
故\(\Delta ABF_1\)的周长为\(|AF_1|+|BF_1|+|AB|=|AF_1|+|BF_1|+|AF_2|+|BF_2|=4a=12\)。
(1). 求椭圆 \(C\) 的方程;
分析: 设椭圆\(C\)的半焦距为\(c\),则由题目可知,\(2a=4\),\(\cfrac{c}{a}=\cfrac{\sqrt{3}}{2}\),
解得\(b^2=1\),\(a^2=4\),故椭圆\(C\) 的方程为\(\cfrac{x^2}{4}+y^2=1\)。
(2). 已知直线 \(l:y=kx-\sqrt{3}\) 与椭圆 \(C\) 交于 \(A,B\) 两点,是否存在实数 \(k\) 使得以线段 \(AB\) 为直径的圆恰好经过坐标原点 \(O\),若存在,求出 \(k\) 的值;若不存在,请说明理由。
分析:存在实数\(k\),使得以线段 \(AB\) 为直径的圆恰好经过坐标原点 \(O\)。理由如下:
设点\(A(x_1,y_1)\),点\(B(x_2,y_2)\),将直线\(l:y=kx-\sqrt{3}\)代入椭圆\(C\) 的方程为\(\cfrac{x^2}{4}+y^2=1\),
整理得到\((1+4k^2)x^2-8\sqrt{3}kx+8=0 (*)\)。
则由韦达定理有\(x_1+x_2=\cfrac{8\sqrt{3}k}{1+4k^2}\),\(x_1x_2=\cfrac{8}{1+4k^2}\),
若以线段 \(AB\) 为直径的圆恰好经过坐标原点 \(O\)由于直径所对的圆周角为直角,故\(\angle AOB=\cfrac{\pi}{2}\),此处可以利用\(\overrightarrow{OA}\)\(\cdot\)\(\overrightarrow{OB}=0\)来刻画垂直,进而说明以线段 \(AB\) 为直径的圆恰好经过坐标原点 \(O\)\(\quad\),则必然满足\(\overrightarrow{OA}\cdot \overrightarrow{OB}=0\),
即\(x_1x_2+y_1y_2=0\),又\(y_1y_2=k^2x_1x_2-\sqrt{3}k(x_1+x_2)+3\)
则有\(\cfrac{8}{1+4k^2}-\cfrac{4k^2-3}{1+4k^2}=0\),解得\(k=\pm \cfrac{\sqrt{11}}{2}\),
经过检验知道,此时\((*)\)式的\(\Delta >0\),满足题意。[若不检验,可能会产生增根];
所以当\(k=\pm \cfrac{\sqrt{11}}{2}\)时,以线段\(AB\)为直径的圆恰好经过坐标原点\(O\)。
(1). 求椭圆\(M\)的方程。
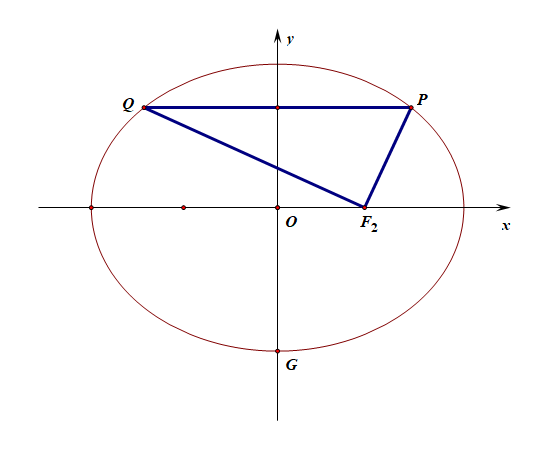
解析:将\(y=\cfrac{3}{\sqrt{7}}\)代入椭圆方程,得到\(x=\pm\cfrac{2}{\sqrt{7}}a\),
故得到\(P(\cfrac{2}{\sqrt{7}}a,\cfrac{3}{\sqrt{7}})\), \(Q(-\cfrac{2}{\sqrt{7}}a,\cfrac{3}{\sqrt{7}})\),\(F(\sqrt{a^2-3},0)\),
这样\(\overrightarrow{PF}=(\sqrt{a^2-3}-\cfrac{2}{\sqrt{7}}a,-\cfrac{3}{\sqrt{7}})\),\(\overrightarrow{QF}=(\sqrt{a^2-3}+\cfrac{2}{\sqrt{7}}a,-\cfrac{3}{\sqrt{7}})\),
由\(\overrightarrow{PF}\cdot\overrightarrow{QF}=0\),得到\(a^2=4\) ,
故椭圆 \(M\) :\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\)。
(2). \(O\)为坐标原点,\(A\)、\(B\)、\(C\)是椭圆\(M\)上不同三点,并且\(O\)是\(\Delta ABC\)的重心,试探究\(\Delta ABC\)的面积是否为定值,若是,求出这个定值;若不是,说明理由。
解析: (有斜率时)设直线 \(AB\) 的方程为 \(y=kx+m\),即\(kx-y+m=0\),
代入椭圆方程 \(3x^{2}+4y^{2}=12\),
可得 \((3+4k^{2})x^{2}+8kmx+4m^{2}-12=0\),
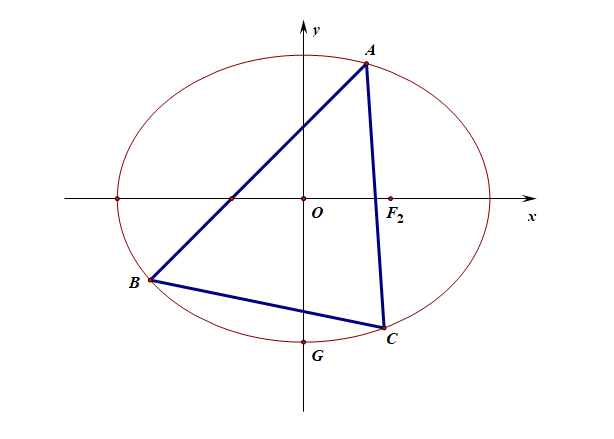
设\(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\),则\(\overrightarrow{OA}=(x_1,y_1)\),\(\overrightarrow{OB}=(x_2,y_2)\),
由韦达定理得到,则 \(x_{1}x_{2}=\cfrac{4m^{2}-12}{3+4k^{2}}\), \(x_{1}+x_{2}=-\cfrac{8km}{3+4k^{2}}\),
\(y_{1}+y_{2}=k(x_{1}+x_{2})+2m=\cfrac{6m}{3+4k^{2}}\),
由 \(O\) 为 \(\triangle ABC\) 的重心, 则\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)
可得 \(\overrightarrow{OC}=-(\overrightarrow{OA}+\overrightarrow{OB})\),又由于\(\overrightarrow{OA}+\overrightarrow{OB}=(x_1+x_2,y_1+y_2)\),
故有\(\overrightarrow{OC}=(\cfrac{8km}{3+4k^{2}},-\cfrac{6m}{3+4k^{2}})\),即点\(C(\cfrac{8km}{3+4k^{2}},-\cfrac{6m}{3+4k^{2}})\)
由于点\(C\)在椭圆上, 则有 \(3(\cfrac{8km}{3+4k^{2}})^{2}+4(-\cfrac{6m}{3+4k^{2}})^{2}=12\),
化简上式,可得 4\(m^{2}=3+4k^{2}\),
又由弦长公式可得,\(|AB|=\sqrt{1+k^{2}}\cdot\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}\)
\(=\sqrt{1+k^{2}}\cdot\sqrt{(-\cfrac{8km}{3+4k^{2}})^{2}-4\cdot\cfrac{4m^{2}-12}{3+4 k^{2}}}\)
\(=\cfrac{4 \sqrt{1+k^{2}}}{3+4k^{2}}\cdot\sqrt{9+12k^{2}-3m^{2}}\)
再者,由点\(C\) 到直线 \(AB\) 的距离 \(d=\cfrac{|kx_{_C}+m-y_{_C}|}{\sqrt{1+k^{2}}}\)
\(=\cfrac{\left|k\cdot \cfrac{8km}{3+4k^{2}}+m-(-\cfrac{6m}{3+4k^{2}})\right|}{\sqrt{1+k^{2}}}=\cfrac{|3m|}{\sqrt{1+k^{2}}}\),
\(S_{\triangle ABC}=\cfrac{1}{2}|AB| \cdot d=\cfrac{1}{2}\cdot\cfrac{4\sqrt{1+k^{2}}}{3+4k^{2}}\cdot\sqrt{9+12k^{2}-3m^{2}}\cdot \cfrac{|3m|}{\sqrt{1+k^{2}}}\)
\(=\cfrac{6|m|}{3+4k^{2}}\cdot\sqrt{9+12k^{2}-3m^{2}}\)\(=\cfrac{6|m|}{4m^{2}}\cdot\sqrt{12m^{2}-3m^{2}}\)
\(=\cfrac{6|m|}{4m^{2}}\cdot |3m|=\cfrac{9}{2}\),
当直线 \(AB\) 的斜率不存在时,要满足条件\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\),

则直线为 \(x=-1\),此时\(A(-1,\cfrac{3}{2})\),\(B(-1,-\cfrac{3}{2})\),\(C(2,0)\),
故 \(|AB|=3\), \(d=2+1=3\), \(S_{\triangle ABC}=\cfrac{1}{2}|AB|\cdot d=\cfrac{9}{2}\).
综上可得, \(\triangle ABC\) 的面积为定值 \(\cfrac{9}{2}\).
(1)求椭圆\(C\)的方程;
分析:由题目可知,\(b=1\),\(c=1\),则\(a^2=2\),
故椭圆方程为\(C:\cfrac{x^2}{2}+y^2=1\);
(2)若斜率为\(k\)的直线过点\(M(2,0)\),且与椭圆\(C\)相交于\(A、B\)两点,试探讨\(k\)为何值时,\(OA\perp OB\)。
分析:设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),直线\(AB\)的方程为\(y=k(x-2)\),
由\(\left\{\begin{array}{l}{y=k(x-2)}\\{\cfrac{x^2}{2}+y^2=1}\end{array}\right.\),消去\(y\)得到,\((1+2k^2)x^2-8k^2x+8k^2-2=0\),
所以\(x_1+x_2=\cfrac{8k^2}{1+2k^2}\),\(x_1x_2=\cfrac{8k^2-2}{1+2k^2}\),
由于\(OA\perp OB\),所以\(x_1x_2+y_1y_2=0\)。
而\(y_1y_2=k^2(x_1-2)(x_2-2)\),所以\(x_1x_2+k^2(x_1-2)(x_2-2)=0\),
即\((1+k^2)x_1x_2-2k^2(x_1+x_2)+4k^2=0\),
所以\(\cfrac{(1+k^2)(8k^2-2)}{1+2k^2}-\cfrac{16k^4}{1+2k^2}+4k^2=0\),
解得\(k^2=\cfrac{1}{5}\),此时\(\Delta >0\),所以\(k=\pm \cfrac{\sqrt{5}}{5}\)。
解:如图所示,由于直线为 \(y=\sqrt{3}(x+c)\),则直线的倾斜角\(\alpha\)满足\(\tan\alpha=\sqrt{3}\),故\(\alpha=\cfrac{\pi}{3}=60^{\circ}\);
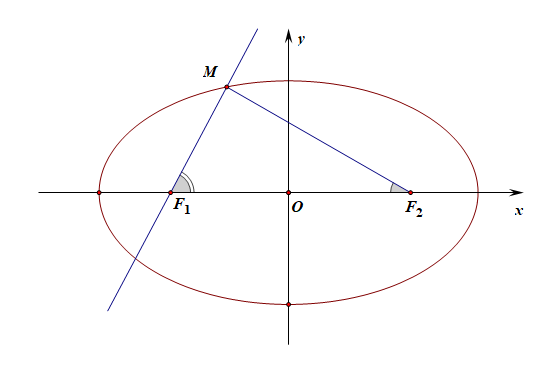
又直线与椭圆 \(C\) 的一个交点为\(M\),满足\(\angle MF_1F_2=2\angle MF_2F_1\),
故 \(\angle MF_{2}F_{1}=30^{\circ}\), 则\(\angle F_{1}MF_{2}=90^{\circ}\),
设 \(|MF_2|=m\), \(|MF_1|=n\),
则\(\left\{\begin{array}{l}m^2+n^2=(2c)^2①&\Leftarrow直角三角形的边的关系\\m+n=2a②&\Leftarrow椭圆的定义\\m=\sqrt{3}n③&\Leftarrow 30^{\circ}、60^{\circ}、90^{\circ}三角形边的关系\end{array}\right.\)
将③代入②,得到\(n=\cfrac{2a}{\sqrt{3}+1}=(\sqrt{3}-1)a\)④,
将③代入①,得到\(4n^2=4c^2\),即\(n^2=c^2\),即\([(\sqrt{3}-1)a]^2=c^2\),
解得\(\cfrac{c}{a}=\sqrt{3}-1\),故椭圆的离心率 \(e=\sqrt{3}-1\). 故答案为 \(\sqrt{3}-1\).
分析:由于\(A_1A_2=2a\),故圆的半径为\(r=a\),由题目圆与直线\(bx-ay+2ab=0\)相切,
则圆心到此直线的距离\(d=r\),即\(\cfrac{|b\times 0-a\times 0+2ab|}{\sqrt{a^2+b^2}}=a\),解得\(a^2=3b^2\),则\(c^2=a^2-b^2=2b^2\),
故\(e^2=\cfrac{c^2}{a^2}=\cfrac{2b^2}{3b^2}=\cfrac{\sqrt{6}}{3}\),故选\(A\)。
分析:椭圆\(\cfrac{x^2}{25}+\cfrac{y^2}{9}=1\)中的最短弦长为通经,最长的弦长为长轴的长,容易计算得到通经长为\(\cfrac{18}{5}=3.6\),则椭圆的弦从最短的弦变化为最长的弦的过程中,得到的好弦的长度分别为\(4\),\(5\),\(6\),\(7\),\(8\),\(9\),\(10\),
而且由于椭圆关于\(x\)轴对称,故有两组,又由于焦点有两个,故还有两组,故共有四组,其和为\((4+5+6\) \(+7+8+9+\) \(10)\times 4\) \(=196\),但是上述的计算过程中将最长的好弦(即长轴)多计算了3次,故所求为\(196-30=166\),故选\(B\)。
(1).求椭圆\(C\)的标准方程;
分析:由于\(S_{\triangle ABF}=1\),则\(\cfrac{1}{2}c\cdot 2b=1\),即\(bc=1\),
又由于\(e=\cfrac{c}{a}=\cfrac{\sqrt{2}}{2}\),\(a^2=b^2+c^2\),
解得\(a^2=2\),\(b^2=1\),即椭圆\(C\)的标准方程为\(\cfrac{x^2}{2}+y^2=1\);
(2).过点\(D(2,0)\)的直线\(l\)与椭圆\(C\)交于不同的两点\(M\),\(N\)(\(M\)在\(D\)、\(N\)之间),求\(\cfrac{S_{\triangle ODM}}{S_{\triangle ODN}}\)(\(O\)为坐标原点)的取值范围;
分析:设\(M(x_1,y_1)\),\(N(x_2,y_2)\),直线\(l\)的方程为\(x=my+2\),与椭圆方程\(\cfrac{x^2}{2}+y^2=1\)联立,
消去\(x\)得到,\((m^2+2)y^2+4my+2=0\),由\(\Delta =8m^2-16>0\),得到\(m^2>2\),
所以\(y_1+y_2=\cfrac{-4m}{m^2+2}\),\(y_1y_2=\cfrac{2}{m^2+2}\),
令\(\cfrac{S_{\triangle ODM}}{S_{\triangle ODN}}=\cfrac{|y_1|}{|y_2|}=t\),由于\(|y_1|<|y_2|\),则有\(0<t<1\),
则\(\cfrac{(y_1+y_2)^2}{y_1y_2}=t+\cfrac{1}{t}+2=\cfrac{8m^2}{m^2+2}=\cfrac{8}{1+\cfrac{1}{m^2}}\in (1,8)\)
即\(3-2\sqrt{2}<t<1\),所以\(\cfrac{S_{\triangle ODM}}{S_{\triangle ODN}}\)的取值范围为\((3-2\sqrt{2},1)\);
分析:设椭圆的左焦点为\(F_1\),则由\(\triangle FOB \cong \triangle F_1OA\),则可知\(|AF_1|=|BF|\),则由\(|AF|+|BF|=6\)结合椭圆的定义,得到\(2a=6\),则\(a=3\),
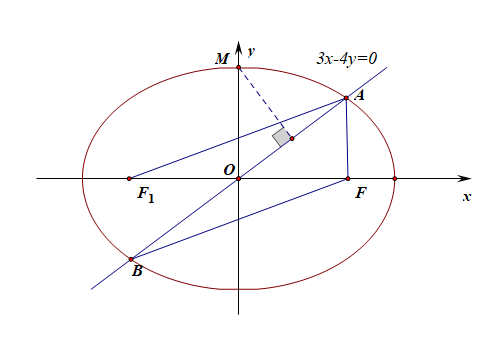
又由于点\(M\)与直线\(l\)的距离不小于\(\cfrac{8}{5}\),得到\(\cfrac{|-4b|}{5}\ge \cfrac{8}{5}\),解得\(b\ge 2\),
则\(e^2=\cfrac{c^2}{a^2}=\cfrac{a^2-b^2}{a^2}=1-\cfrac{b^2}{9}\leq 1-\cfrac{4}{9}=\cfrac{5}{9}\),故\(0<e\leq \cfrac{\sqrt{5}}{3}\)。故选\(B\)。
分析:设\(M(x_1,y_1)\),\(N(x_2,y_2)\),线段\(MN\)的中点\(P(x_0,y_0)\),
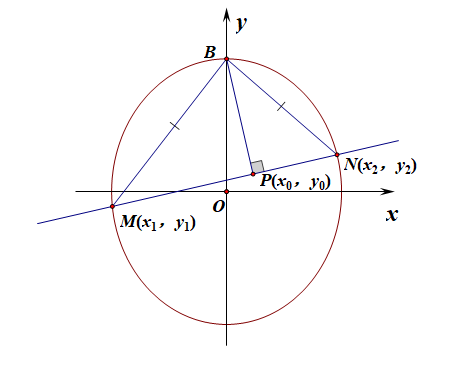
则由\(b^2x_1^2+y_1^2=b^2\)①,\(b^2x_2^2+y_2^2=b^2\)②,且有\(\cfrac{y_2-y_1}{x_2-x_1}=1\),
由点差法,①-②得到,\(b^2(x_1+x_2)=-(y_1+y_2)\),即\(x_0b^2=-y_0\)③,
又\(|BM|=|BN|\),则\(BP\perp MN\),\(k_{BP}=-1=\cfrac{y_0-b}{x_0}\)④,
由③④可得,\(x_0=\cfrac{b}{1-b^2}\),\(y_0=\cfrac{b^3}{1-b^2}\),由于点\(P(\cfrac{b}{1-b^2},\cfrac{b^3}{1-b^2})\)在椭圆内,
故\(\cfrac{b^2}{(1-b^2)^2}+\cfrac{\frac{b^6}{(1-b^2)^2}}{b^2}<1\),
解得\(3b^2<1\),又\(b>0\),故\(0<b<\cfrac{\sqrt{3}}{3}\)。
解后反思:①出现这种范围问题的求解策略,其一,联立求解\(\Delta >0\);其二,点\(P(x_0,y_0)\)在椭圆内,则\(\cfrac{x_0^2}{a^2}+\cfrac{y_0^2}{b^2}<1\),
②涉及到与圆锥曲线相交的直线的斜率、中点问题常常考虑使用点差法。



 收集整理与椭圆有关的习题
收集整理与椭圆有关的习题
